Vitesse et consommation d'énergie

Un constructeur automobile conçoit une nouvelle voiture électrique. Il souhaite optimiser la vitesse pour que la consommation d’énergie soit la plus faible possible. Des tests ont permis de modéliser la consommation d’énergie (en kWh/km) en fonction de la vitesse \(v\) (en km/h) avec la fonction \(C(v)=0{,}01v^2−0{,}5v+10\) définie sur \([0;100]\).

Problématique : comment déterminer la vitesse à laquelle la voiture consomme le moins d’énergie ?

1. À quoi correspond la fonction \(C\) ? Que représente la variable \(v\) ?

2. Calculer \(C(10)\) et conclure.

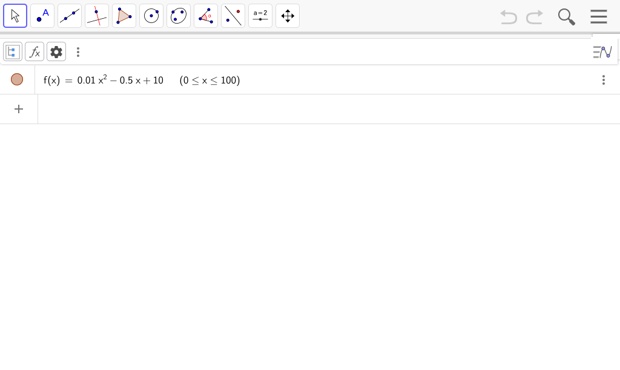
3. Le problème est modélisé par la fonction \(f\) telle que : \(f(x)=0{,}01x^2−0{,}5x+10\) définie sur l'intervalle \([0;100]\).

On se propose d'étudier le comportement du nombre dérivé en plusieurs points de la courbe de la fonction \(f\) à l'aide de GeoGebra.

Tutoriel : aller dans la perle "Vitesse et consommation d'énergie - Tutoriel" et réaliser les manipulations demandées.

4. Que constate-t-on lorsqu'on affiche la trace du point P ?

5. Dans GeoGebra

• Dans la fenêtre algèbre, taper la commande "Dérivée (fonction)".
• Saisir Dérivée (f).

Que constate-t-on ?

6. Donner l'expression de la fonction dérivée de \(f\) que l'on nommera \(f'\) puis en déduire une expression dérivée de la fonction \(C\).

7. La fonction dérivée correspond ici à la variation de la consommation en fonction de la vitesse. La consommation est minimale lorsque la dérivée s'annule. 

Résoudre l'équation \(C'(v)= 0\).

8. En déduire  la vitesse à laquelle la voiture consomme le moins d'énergie.

9. Répondre à la problématique.